Propiedades de las Potencias
Potencias con exponente uno
Cualquier valor elevado a 1, da como resultado el mismo valor:
![]()
Esta propiedad es muy útil sobre todo cuando nos aparece un número o variable que no tiene exponente. En ese caso, sabemos que está elevada a 1 gracias a esta propiedad.
Ejemplo:![]()
Potencias con exponente cero
Cualquier valor elevado a 0, tiene como resultado 1![]()
Mucho cuidado con esta propiedad porque es muy común confundirse y pensar que cuando un número o variable está elevada a 0 es 0. Eso es un grave error.
Ejemplo:

No tiene por qué ser solo un número o una variable. Cualquier operación que esté elevada a 0, el resultado también es 1. Da igual lo que sea.
Multiplicación de potencias con la misma base
Multiplicación de potencias con la misma base: Se mantiene la base y se suman los exponentes:
![]()
Ejemplo:![]()
¿Qué pasa si tienen distinta base? Si tienen distinta base no se puede utilizar esta propiedad:
![]()
División de potencias con la misma base
División de potencias con la misma base: Se mantiene la base y se restan los exponentes:
 Ejemplo:
Ejemplo:
Al igual que ocurre con la propiedad anterior, esta propiedad no se aplica si las potencias tienen distinta base.
Multiplicación elevada a una potencia
Cuando tenemos una multiplicación elevada a un exponente, el resultado es igual a cada factor elevado a ese mismo exponente:
![]()
Esta propiedad se aplica con variables para eliminar los paréntesis:

También puede utilizarse con números, pero en sentido inverso, es decir, cuando tenemos dos números con el mismo exponente:
![]()
¡Mucho cuidado! Esta propiedad sólo funciona con la multiplicación. No funciona con sumas y restas.
![]()
![]()
Para resolver las sumas y restas al cuadrado utilizamos los productos notables.
Cociente elevado a una potencia
Cociente elevado a una potencia: Es igual al numerador y al denominador elevados a la misma potencia:
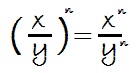
Propiedad muy útil para eliminar paréntesis en expresiones más complejas:
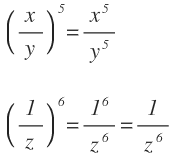
O si trabajamos con números, nos sirve para calcular el resultado:

Si podemos operar dentro del paréntesis, también podemos resolver la potencia sin aplicar esta propiedad, solamente resolviendo el paréntesis y después elevarlo al exponente:
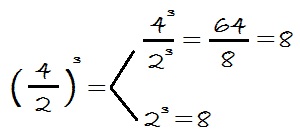
Potencia de otra potencia
Potencia elevada a otra potencia: Se mantiene la base y se multiplican los exponentes:
![]()
Puedes encontrarte la potencia de potencia sin paréntesis, pero eso no es lo correcto. Debe llevar paréntesis para indicar que se está elevando toda la potencia a otra potencia.
Ejemplo:![]()
Esta propiedad se combina con las dos propiedades anteriores.
Cuando tenemos una multiplicación o división de potencias, elevadas a otra potencia, el exponente de fuera multiplica a cada uno de los exponentes de dentro del paréntesis.
Con la multiplicación:
![]()
Por ejemplo:
![]()
Y con la división:

Por ejemplo:

Potencias con exponente negativo
Potencias de exponente negativo: Un valor elevado a una potencia negativa, es equivalente a 1 dividido entre el valor elevado a la misma potencia positiva:

Ejemplo:
Como caso particular de esta propiedad esta la inversa de un número, que es cualquier valor elevado a -1:
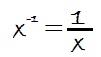
Fracción elevado a exponente negativo: En este caso se le da la vuelta a la fracción y el exponente se pone positivo:

Potencia de exponente racional
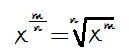 Ejemplo:
Ejemplo:
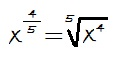
El denominador del exponente se convierte en el índice de la raíz
Potencia de exponente racional y negativo
 Ejemplo:
Ejemplo: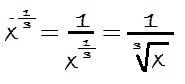

No hay comentarios:
Publicar un comentario